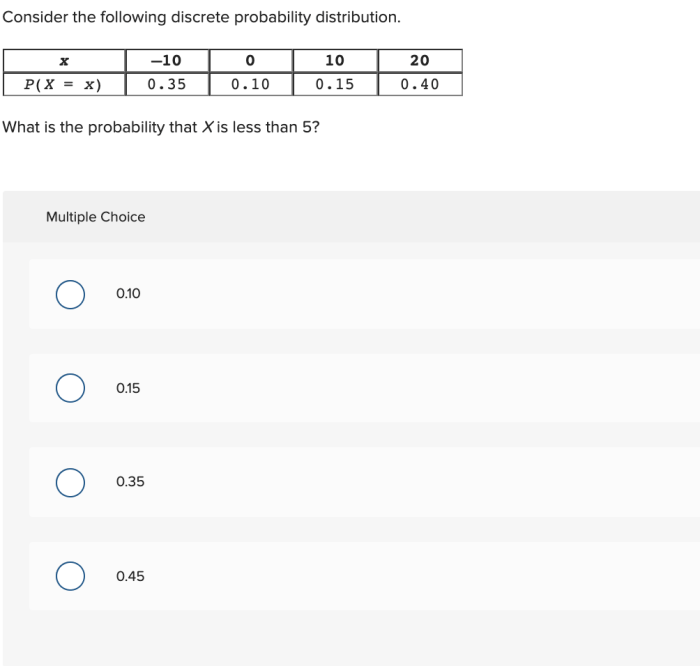
Consider the following discrete probability distribution: a fundamental concept in probability theory that governs the likelihood of discrete outcomes. This distribution plays a crucial role in various fields, from statistics and engineering to finance, enabling us to model real-world phenomena and make informed decisions.
Delving into the intricacies of discrete probability distributions, we will explore the probability mass function, cumulative distribution function, expected value, and variance. We will also examine common discrete distributions such as the binomial, Poisson, and geometric distributions, highlighting their characteristics and applications.
Discrete Probability Distributions: Consider The Following Discrete Probability Distribution
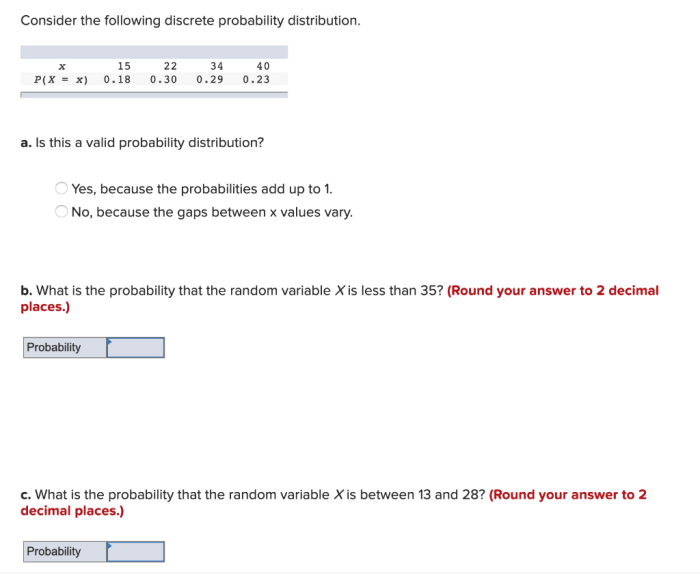
Discrete probability distributions describe the probabilities of different outcomes in an experiment with a finite number of possible outcomes. They are used in various fields, including statistics, engineering, and finance, to model and analyze data.
Probability Mass Function (PMF)
The probability mass function (PMF) of a discrete probability distribution is a function that assigns a probability to each possible outcome. It is defined as follows:
P(X = x) = probability of outcome x
The PMF must satisfy the following properties:
- Non-negativity: P(X = x) ≥ 0 for all x
- Sum to 1: Σ xP(X = x) = 1
Cumulative Distribution Function (CDF)
The cumulative distribution function (CDF) of a discrete probability distribution is a function that gives the probability that the random variable X takes on a value less than or equal to a given value x. It is defined as follows:
F(x) = P(X ≤ x) = Σy ≤ xP(X = y)
The CDF has the following properties:
- Monotonicity: F(x) is increasing for all x
- Right-continuity: F(x) is right-continuous for all x
Expected Value and Variance
The expected value of a discrete probability distribution is the average value of the random variable. It is defined as follows:
E(X) = ΣxxP(X = x)
The variance of a discrete probability distribution is a measure of how spread out the distribution is. It is defined as follows:
Var(X) = Σx(x
E(X))2P(X = x)
Common Discrete Probability Distributions
There are several common discrete probability distributions that are used in practice:
- Binomial distribution: models the number of successes in a sequence of independent experiments
- Poisson distribution: models the number of events that occur in a fixed interval of time or space
- Geometric distribution: models the number of trials until the first success in a sequence of independent experiments
Applications of Discrete Probability Distributions, Consider the following discrete probability distribution
Discrete probability distributions have a wide range of applications in various fields:
- Statistics: hypothesis testing, confidence intervals, regression analysis
- Engineering: reliability analysis, queuing theory, inventory management
- Finance: risk assessment, portfolio optimization, insurance pricing
FAQ
What is a discrete probability distribution?
A discrete probability distribution is a function that assigns probabilities to each possible outcome of a discrete random variable.
What is the probability mass function (PMF) of a discrete probability distribution?
The PMF of a discrete probability distribution is a function that gives the probability of each possible outcome.
What is the cumulative distribution function (CDF) of a discrete probability distribution?
The CDF of a discrete probability distribution is a function that gives the probability that a random variable takes on a value less than or equal to a given value.